Forecasting Method for The ATAforecasting

ATA.Forecast is a generic function for forecasting of the ATA Method.

Usage

ATA.Forecast(
  object,
  h = NULL,
  out.sample = NULL,
  ci.level = 95,
  negative.forecast = TRUE,
  onestep = FALSE,
  print.out = TRUE
)

Arguments

object: An ata object is required for forecast.
h: Number of periods for forecasting.
out.sample: A numeric vector or time series of class ts or msts for out-sample.
ci.level: Confidence Interval levels for forecasting. Default value is 95.
negative.forecast: Negative values are allowed for forecasting. Default value is TRUE. If FALSE, all negative values for forecasting are set to 0.
onestep: Default is FALSE. if TRUE, the dynamic forecast strategy uses a one-step model multiple times (h forecast horizon) where the prediction for the prior time step is used as an input for making a prediction on the following time step.
print.out: Default is TRUE. If FALSE, forecast summary of ATA Method is not shown.

Value

An object of class ata and forecast values.

References

#'Yapar G, Yavuz I, Selamlar HT (2017). “Why and How Does Exponential Smoothing Fail? An In Depth Comparison of ATA-Simple and Simple Exponential Smoothing.” Turkish Journal of Forecasting, 1(1), 30–39.

#'Yapar G, Capar S, Selamlar HT, Yavuz I (2018). “Modified Holt's Linear Trend Method.” Hacettepe University Journal of Mathematics and Statistics, 47(5), 1394–1403.

#'Yapar G (2018). “Modified simple exponential smoothing.” Hacettepe University Journal of Mathematics and Statistics, 47(3), 741–754.

#'Yapar G, Selamlar HT, Capar S, Yavuz I (2019). “ATA method.” Hacettepe Journal of Mathematics and Statistics, 48(6), 1838-1844.

Author

Ali Sabri Taylan and Hanife Taylan Selamlar

Examples

trainATA <-  head(touristTR, 84)
ata_fit <- ATA(trainATA, parPHI = 1, seasonal.test = TRUE, seasonal.model = "decomp")

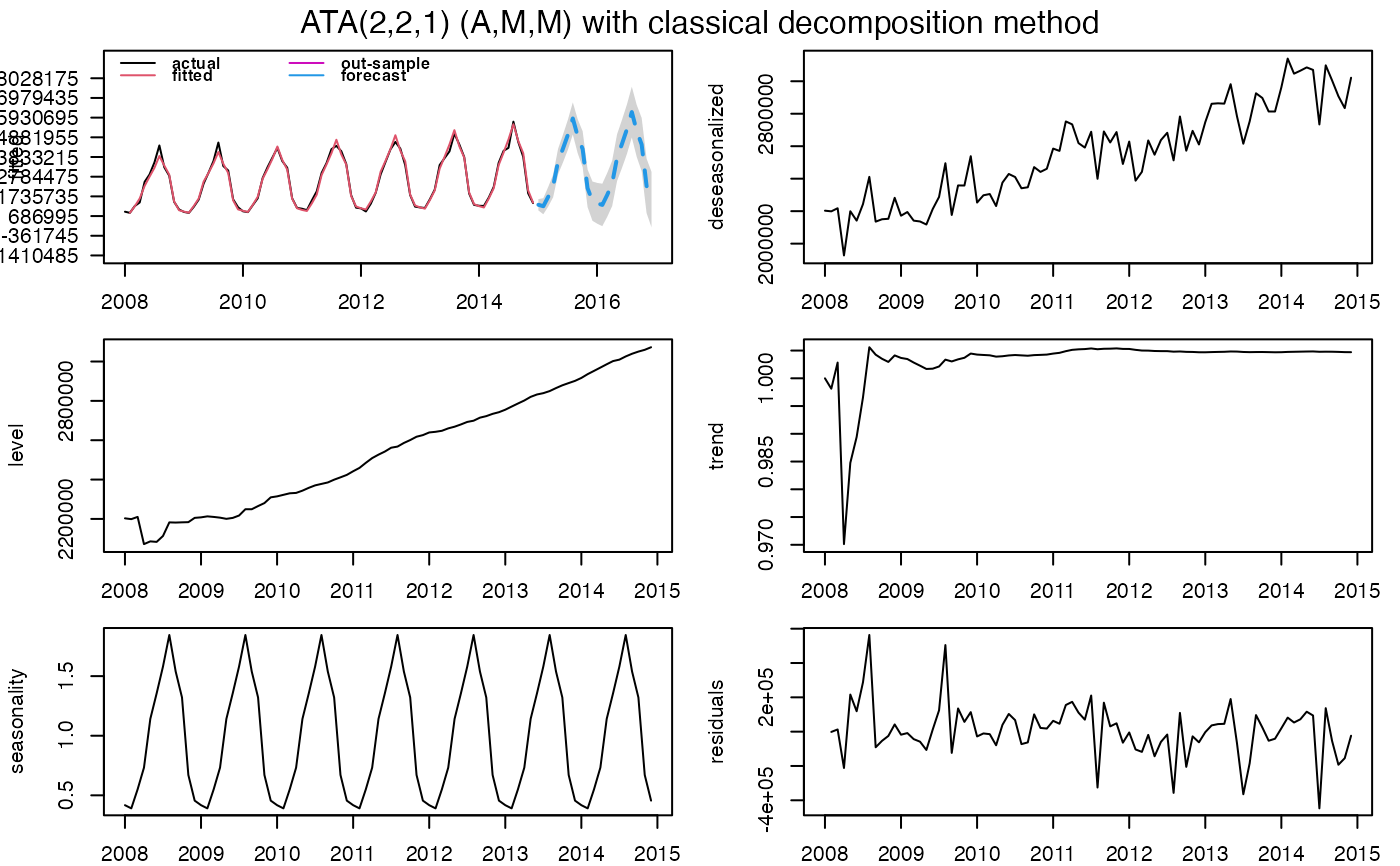#> ATA(2,2,1) (A,M,M) 
#> 
#>    model.type: M 
#> 
#>    seasonal.model: decomp 
#> 
#>    seasonal.type: M 
#> 
#>    forecast horizon: 24 
#> 
#>    accuracy.type: sMAPE 
#> 
#> Model Fitting Measures: 
#> 
#>               sigma2               loglik                  MAE 
#> 25327678645.19519043       -1188.55670094      106527.45549230 
#>                  MSE                 RMSE                  MPE 
#> 23496762116.62686157      153286.53599265           0.12753452 
#>                 MAPE                sMAPE                 MASE 
#>           4.04068178           4.04508846           0.23313082 
#>                  OWA 
#>           0.00000468 
#> 
#> In-Sample Accuracy Measures: 
#> 
#>               MdAE               MdSE              RMdSE               MdPE 
#>      67333.7563803 4533834748.2853584      67333.7563803          0.4018348 
#>              MdAPE             sMdAPE 
#>          3.2125716          3.2275752 
#> 
#> Out-Sample Accuracy Measures: 
#> 
#>   MAE   MSE  RMSE   MPE  MAPE sMAPE  MASE   OWA 
#>    NA    NA    NA    NA    NA    NA    NA    NA 
#> 
#> Out-Sample Accuracy Measures: 
#> 
#>   MdAE   MdSE  RMdSE   MdPE  MdAPE sMdAPE 
#>     NA     NA     NA     NA     NA     NA 
#> 
#> Information Criteria: 
#> 
#>      AIC     AICc      BIC 
#> 2391.113 2392.587 2408.129 
#> 
#> 
#>    user  system elapsed 
#>   0.081   0.083   0.313 
#> 
#> calculation.time: 0.3127 
#> 
#> 
#> Forecasts: 
#> Time Series:
#> Start = 2015.00694444444 
#> End = 2016.92361111111 
#> Frequency = 12 
#>  [1] 1288568 1211322 1716223 2292963 3589547 4283724 5018661 5887346 4933780
#> [10] 4253560 2170497 1480814 1363260 1281536 1815704 2425875 3797616 4532031
#> [19] 5309568 6228607 5219767 4500118 2296310 1566650
#> 
#> 
ata_fc <- ATA.Forecast(ata_fit, h=12)
#> Time Series:
#> Start = 2015.00694444444 
#> End = 2015.92361111111 
#> Frequency = 12 
#>        lower forecast   upper
#> 2015  969867  1271754 1573641
#> 2015  768220  1195153 1622086
#> 2015 1169918  1692802 2215686
#> 2015 1657210  2260985 2864759
#> 2015 2863372  3538412 4213452
#> 2015 3481949  4221419 4960888
#> 2016 4145447  4944165 5742884
#> 2016 4944330  5798196 6652062
#> 2016 3951934  4857595 5763257
#> 2016 3231957  4186608 5141259
#> 2016 1134438  2135685 3136931
#> 2016  410853  1456621 2502389